Calculs statistiques : effectifs et fréquences

Exemple 1
Marie a lancé 20 fois un dé à six faces. Voici les nombres qui sont sortis :
2 – 6 – 5 – 2 – 4 – 1 – 6 – 3 – 1 – 4 – 2 – 1 – 6 – 5 – 6 – 3 – 2 – 1 – 2 – 4.
Ce relevé s’appelle une série statistique.
On réunit ces résultats dans un tableau d’effectifs en regroupant les valeurs de dés :

nombre	1	2	3	4	5	6	total
effectif	4	5	2	3	2	4	20

Par exemple, l’effectif de la valeur « 4 » est de 3. Ceci veut dire que le nombre 4 est sorti 3 fois.
L’effectif total est de 20 lancers.

Exemple 2 : Regroupement par classes
Lorsque les données statistiques sont nombreuses, elles peuvent être regroupées en classes pour faciliter leur lecture.
On a relevé les tailles de 250 hommes adultes. Les tailles varient entre 155 cm et 194 cm. Le tableau utilisé pour présenter ces données comportera 40 catégories de taille et sera difficile à interpréter.

taille (en cm)	155	156	157	158	159	160	...	193	194
effectif	1	2	1	3	5	6	...	2	1

Dans ce cas, il faut regrouper les tailles en classes :

taille (en cm)	155 à 159	160 à 164	165 à 169	170 à 174
effectif	12	30	48	61

 

taille (en cm)	175 à 179	180 à 184	185 à 189	190 à 194
effectif	50	26	17	6

On obtient l’effectif de la classe « 155 à 159 » en additionnant les effectifs inscrits dans les cases bleues du premier tableau (1 + 2 + 1 + 3 + 5 = 12).
 
Ce tableau est plus facile à lire et donne une vision globale des résultats de l’enquête. Cependant, nous perdons des informations. Par exemple, on ne sait plus précisément quelle est la taille de chacune des 12 personnes de la classe « 155 à 159 ».

Exemple 1 : Lancers de dés
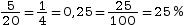Dans l’exemple du lancer de dés précédent, on obtient le tableau des fréquences suivant :

nombre	1	2	3	4	5	6	total
effectif	4	5	2	3	2	4	20
fréquence							1
	0,2	0,25	0,1	0,15	0,1	0,2	1
	20 %	25 %	10 %	15 %	10 %	20 %	100 %

 
Calculs
Dans cette série statistique, le chiffre « 2 » est sorti 5 fois. La fréquence de la valeur « 2 » est donc : .

Exemple 2 : Regroupements en classes
D’après l’exemple vu précédemment, on a le tableau de fréquences suivant :

taille (en cm)	155 à 159	160 à 164	165 à 169	170 à 174
effectif	12	30	48	61
fréquence	= 4,8 %	= 12 %	= 19,2 %	= 24,4 %

 

taille (en cm)	175 à 179	180 à 184	185 à 189	190 à 194
effectif	50	26	17	6
fréquence	= 20 %	= 10,4 %	= 6,8 %	= 2,4 %

 
Calculs
Il y a 50 hommes sur 250 qui mesurent entre 175 et 179 cm. La fréquence de la classe « 175 à 179 cm » est donc : .

Sur l’exemple du dé, la somme des fréquences d’apparition des faces du dé est :
0,2 + 0,25 + 0,1 + 0,15 + 0,1 + 0,2 = 1.