Statistiques : effectifs, moyenne, fréquences, diagrammes
- Fiche de cours
- Quiz
- Profs en ligne
- Videos
- Application mobile
Objectifs
En statistique, on manipule parfois de très grandes
quantités d’informations. Pour en simplifier
l’analyse, on peut effectuer quelques calculs ou
diagrammes : moyennes, fréquences, diagrammes en
bâtons ou circulaires, etc.
Comment calculer des moyennes, des effectifs cumulés, des fréquences, etc. ? Comment représenter ces données sur des graphiques en bâtons ou circulaires ?
Comment calculer des moyennes, des effectifs cumulés, des fréquences, etc. ? Comment représenter ces données sur des graphiques en bâtons ou circulaires ?
1. Études statistiques
On effectue une étude statistique par le
relevé de certaines données sur une
population.
Les données sont, suivant les besoins, sous forme de listes, de tableaux d’effectifs ou de diagrammes.
À partir de ces données, on effectue des calculs qui nous renseignent sur cette étude.
Les données sont, suivant les besoins, sous forme de listes, de tableaux d’effectifs ou de diagrammes.
À partir de ces données, on effectue des calculs qui nous renseignent sur cette étude.
a. Moyenne pondérée
La moyenne pondérée donne « un
aperçu » d’une série
statistique.
La moyenne est un indicateur de « position » d’une série statistique.
Elle est donnée par la formule :
La moyenne est un indicateur de « position » d’une série statistique.
Elle est donnée par la formule :
Moyenne pondérée =
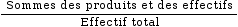
b. Fréquence d'une valeur
La fréquence d'une valeur est un indicateur du
nombre de fois par rapport à la totalité
qu’une valeur est présente dans une série
statistique.
La fréquence est un nombre compris entre 0 et 1 que l’on peut aussi donner sous forme de pourcentages.
Elle est donnée par la formule suivante :
La fréquence est un nombre compris entre 0 et 1 que l’on peut aussi donner sous forme de pourcentages.
Elle est donnée par la formule suivante :
Fréquence d'une valeur =
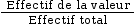
c. Fréquences cumulées
Les fréquences cumulées permettent de
répondre facilement à des questions
« Quel pourcentage de la population a moins de
(ou a plus de), etc. ? ».
Pour y répondre, on distingue :
Pour y répondre, on distingue :
- les fréquences cumulées croissantes associées à une valeur est la somme des fréquences des valeurs inférieures ;
- Les fréquences cumulées décroissantes associées à une valeur est la somme des fréquences des valeurs supérieures.
2. Étude statistique sur des valeurs discrètes
- Exemple
Dans une classe de 25 élèves, on a
répertorié le nombre de frères et sœurs
de chaque élève dans un tableau.
| Nombre de frères et sœurs | 0 | 1 | 2 | 3 | 4 | Total |
| Effectif | 2 | 8 | 9 | 5 | 1 | 25 |
a. Moyenne pondérée
Moyenne pondérée = 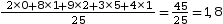
En moyenne, les élèves de cette classe ont un peu moins de 2 frères et sœurs.
En moyenne, les élèves de cette classe ont un peu moins de 2 frères et sœurs.
b. Fréquences et fréquences cumulées
croissantes
| Nombre de frères et sœurs | 0 | 1 | 2 | 3 | 4 | Total |
| Effectif | 2 | 8 | 9 | 5 | 1 | 25 |
| Fréquence en pourcentage (en %) | 8 | 32 | 36 | 20 | 4 | 100 |
| Fréquence cumulée croissante (en %) | 8 | 40 | 76 | 96 | 100 | - |
-
Fréquence en % de la valeur
« 3 frères et »
Fréquence =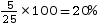
Donc 20 % des élèves de cette classe ont 3 frères ou sœurs. -
Pourcentage d’élèves ayant
au plus
2 frères et sœurs
D’après le tableau de fréquences cumulées croissantes, on peut lire qu’il y a 76 % des élèves de cette classe qui ont au plus 2 frères et sœurs.
Pour obtenir ce résultat, on additionne toutes les fréquences des valeurs inférieures ou égales à 2 frères et sœurs : Soit 8 + 32 + 36 = 76 %.
c. Diagramme en bâtons
Pour mieux visualiser cette étude statistique, on
peut tracer un diagramme en bâtons.


3. Étude statistique sur des valeurs données
par classe - Exemple
Dans la même classe de 25 élèves, on note la
taille des élèves dans un tableau en les
regroupant par classe.
Les intervalles [150 ; 160[ ou [160 ; 170[ sont, par exemple, des classes de valeurs.
| Taille en cm | [150 ; 160[ | [160 ; 170[ | [170 ; 180[ | [180 ; 190[ |
| Effectif | 3 | 11 | 8 | 3 |
| Centre de classe | 155 | 165 | 175 | 185 |
Les intervalles [150 ; 160[ ou [160 ; 170[ sont, par exemple, des classes de valeurs.
a. Moyenne pondérée
Pour calculer la moyenne pondérée d’une
étude statistique donnée par classe, on utilise
le centre de la classe :
Moyenne pondérée =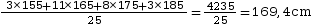
En moyenne, les élèves de cette classe mesurent 169,4 cm.
Moyenne pondérée =
En moyenne, les élèves de cette classe mesurent 169,4 cm.
Remarque :
Ce calcul de moyenne n'est pas très précis. Avec la technique utilisée précédemment, on considère en effet que les 3 élèves de la classe [150 ; 160[ mesurent tous 155 cm, ce qui peu probable.
Pour avoir une moyenne plus précise, il aurait fallu connaitre la taille exacte de chacun des élèves.
Ce calcul de moyenne n'est pas très précis. Avec la technique utilisée précédemment, on considère en effet que les 3 élèves de la classe [150 ; 160[ mesurent tous 155 cm, ce qui peu probable.
Pour avoir une moyenne plus précise, il aurait fallu connaitre la taille exacte de chacun des élèves.
b. Fréquence d'une valeur
Pourcentage d’élèves mesurant
entre 160 et 170 cm : Il y a 11
élèves sur 25 qui sont dans cette tranche
de taille.
Soit :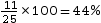
Donc 44 % des élèves de cette classe mesurent entre 160 et 170 cm.
Soit :
Donc 44 % des élèves de cette classe mesurent entre 160 et 170 cm.
c. Diagramme circulaire
Pour mieux représenter cette étude statistique,
on peut tracer un diagramme circulaire.
On établit pour cela le tableau qui donne les angles correspondants aux effectifs pour chaque classe de taille.
On établit pour cela le tableau qui donne les angles correspondants aux effectifs pour chaque classe de taille.
| Taille en cm | [150 ; 160[ | [160 ; 170[ | [170 ; 180[ | [180 ; 190[ |
| Effectif | 3 | 11 | 8 | 3 |
| Angle (en degrés) | 43,2° | 158,4° | 115,2° | 43,2° |
Exemple de calculs d’angles :
Angle correspondant aux 3 élèves mesurant entre 150 et 160 cm :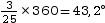

Angle correspondant aux 3 élèves mesurant entre 150 et 160 cm :

Vous avez obtenu75%de bonnes réponses !







